La extraña conexión entre la revolución rusa y las matemáticas detrás de la inteligencia artificial

En 1905 estalló en Rusia la revolución.

Se le llamó la "primera revolución rusa", y culminó con el Zar Nicolás II concediendo a la creación de una constitución y de la creación del primer parlamento (Duma).

El conflicto dividió al país entre aquellos que querían proteger al status quo y querían que permaneciera un gobierno con un Zar en el poder, y los comunistas, que deseaban un gobierno más democrático.

En un lado: marxismo, materialismo dialéctico, ateismo. En el otro: religión, filosofía clásica y una mentalidad burguesa.

Del lado religioso se encontraba Pavel Nekrasov (Павел Алексеевич Некрасов), que como cristiano Ortodoxo, rechazaba al materialismo de Marx y era un fiel creyente del libre albedrío. La cuestión es filosófica, pero él y otros matemáticos estaban convencidos de que se trataba de una cuestión que se podía comprobar con matemáticas.

En particular, observando que la ley de los números grandes se cumple en las ciencias sociales

En 1713, Bernoulli encontró que si lanzas una moneda suficientes veces, la probabilidad observada de cualquier lado de la cara se acercará cada vez más al 50% (asumiendo que la moneda es justa). A este fenómeno se le llamó la ley de los grandes números.

Durante muchos años, este era el principio fundamental de la estadística. Y para que esta ley se cumpliera, cada lanzamiento de la moneda tenía que ser completamente independiente del que le sigue.

Este principio lo podemos observar en diferentes aspectos de la sociedad. Por ejemplo, en esta tabla están los matrimonios en Bélgica de 1841 a 1845 (Seneta, 2007).

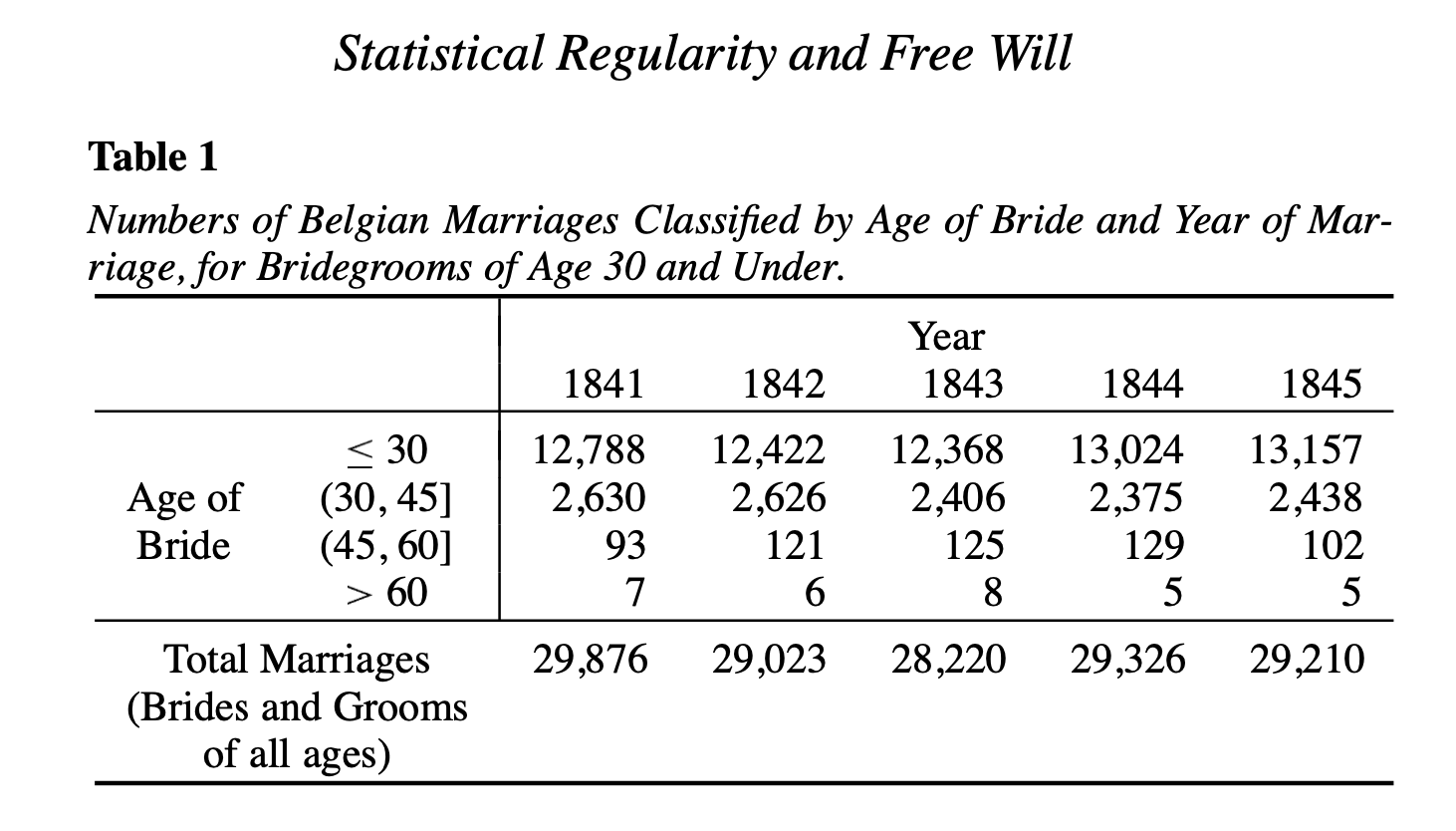
Es difícil imaginar un acto de libre albedrío más representativo que el matrimonio. Las personas no tienen un mandato gubernamental ni un imperativo que les indique a qué edad deben de casarse. Las personas se casan cuando ellas quieren y con quien quieren, ¿cierto?

Y aún así, los números que se ven en esa tabla son casi idénticos año por año.

Para Nekrasov, y otros pensadores similares de la época, esta era una prueba infalible de que, si la ley de los grandes números está presente en las decisiones sociales, entonces esa es una prueba de la existencia de independencia estadística y, con ella, del libre albedrío. Observó que los números seguían patrones similares en las tasas de nacimiento e incluso las tasas de crímenes. Son decisiones que toman las personas de forma independiente y que convergen en cifras de la misma manera en la que la una moneda cae la mitad de las veces de una cara y la mitad de las veces de otra.

Y, si estos fenómenos seguían la ley de los grandes números, entonces debían de provenir de actos independientes… es decir, del libre albedrío.

Pero para Andrey Markov, eso era un abuso de las matemáticas

Del otro lado estaba Markov. Le decían Andrey el furioso… y no estaba nada contento con la conclusión de Nekrasov.

Desde su punto de vista, decir que la independencia estadística implica el libre albedrío era un sinsentido.

Así que se puso manos a la obra en una demostración de que hay eventos dependientes que también siguen la ley de los grandes números. Para lograrlo, quiso emplear un ejemplo en el que un evento claramente dependa de los eventos anteriores. Y un gran ejemplo es en el texto. Si la siguiente letra es una vocal o una consonante, depende fuertemente de la letra anterior. Cada letra depende la anterior.

Así que tomó “Eugenio Onegin”, una novela clásica de Alexander Pushkin, extrajo las primeras 20 mil letras del poema y las puso en una “cadena” de letras sin puntuaciones ni espacios. Encontró que un 43% eran vocales y el 57% restante eran consonantes y luego calculó la probabilidad de las transiciones de vocales a consonantes y entre si.

Por ejemplo, si 43% eran vocales, entonces la probabilidad de transición entre una vocal y otra debería ser .43x.43=0.185, o 18.5%. Sin embargo, la probabilidad real de que una letra sea una vocal dado que la anterior era una vocal era realmente de 6%.

Lo mismo pasó con los otros tres tipos de transición. Los valores de las probabilidades diferían mucho de lo que deberían ser si fueran variables independientes. Así fue que Markov comprobó que las letras tenían un comportamiento dependiente, ahora solo quedaba demostrar que seguían la ley de los grandes números.

La máquina de la predicción

Puso dos estados: vocales y consonantes. Para calcular la probabilidad de que una vocal pase a ser una vocal incorporó el porcentaje de aparición de vocales (0.06/0.43=0.14) y calculó un 14%. Y, como todas las probabilidades tenían que sumar un 100%, la probabilidad de que se pase de una vocal a una consonante era (1-0.14 = 0.87) 87%.