La ecuación mas bella del mundo

La realidad: los símbolos matemáticos se ven increíbles en nuestro cuerpo como tatuajes.

La única razón por la que no los usamos más seguido es porque ¡qué pena tatuarnos algo que no sea correcto! Es como cuando el tatuaje en Chino resulta en palabras que no nos tatuaríamos en nuestro idioma. De ese caso, ejemplos abundan.

En agosto me hice una cita para hacerme un retoque en mi tatuaje, y platicando con mi tatuador, le mencioné un poco sobre lo que hago y vi cómo se le iluminaron los ojos de inspiración. Guardó esto como nota de lo que hará: Números binarios - representaciones matemáticas.

De inmediato pensé dos cosas:

1. Qué bien que entendió lo que quiero para mi tatuaje.
2. Pero… ¿él qué entiende por “representaciones matemáticas”?

Y como una gran parte de las personas en el mundo sienten ñáñaras cuando les hablas de matemáticas, me temo que simplemente irá a Pinterest y me arriesgo a acabar con el equivalente matemático a tatuarme “caldo de pollo” en chino por todo mi pecho.

Esta es una guía para ayudar a los tatuadores no-matemáticos a hacer tatuajes inspirados en las matemáticas y para personas que desean hacerse un tatuaje inspirado en las matemáticas y no quieren terminar haciendo el ridículo en las pool party de los congresos de matemáticas.

Las matemáticas son extremadamente bellas por si mismas. Apreciar la belleza matemática activa las mismas regiones en el cerebro que apreciar un gran arte o una pieza musical (Zeki, 2014). Estoy seguro de que son muchas más personas las que desean plasmar esa belleza en el cuerpo en la forma de un tatuaje.

En las siguientes secciones presentaré algunas de las representaciones que a mi parecer se prestan de manera natural para una representación en forma de tatuaje, ya sea porque son símbolos que por sí mismos se ven atractivos y estéticos o porque lo que representan es muy profundo.

Lo más común es que se cumplan esas dos características.

La ecuación mas bella del mundo

Hay dos razones para tatuarse algo matemático: por el significado y el efecto visual.

Hay expresiones que cargan mucho significado, pero que no se ven en esencia complejas. Por ejemplo:

$$e^{\pi i} + 1 = 0$$

Es considerada una de las ecuaciones más bellas que existen. Se llama la identidad de Euler, en honor a uno de los matemáticos más brillantes que han existido en este planeta. Se considera bella porque unifica cinco símbolos matemáticos fundamentales en una sola ecuación (Geiger, 2013).

• Los números 1 y 0 son la base de todos los números. Son la base del sistema binario y son la identidad de la multiplicación y la suma, respectivamente.
• El número pi. Tal vez lo conoces porque te obligaron a aprender que es 3.141592... se trata de la relación entre la circunferencia de un círculo y su diámetro. En palabras sencillas, si tomas el diámetro de una rueda con un hilo, ese hilo tendrá que pasar poco más de 3 veces para rodear esa misma rueda, sin importar su tamaño. Es una proporción muy bella e interesante. También es interesante por ser de esos números que se conocen como irracionales y tiene otras propiedades muy interesantes.
• El número e, también conocido como el número Euler (si estás en matemáticas más de dos minutos, vas a escuchar ese nombre muy seguido), es la base de los logaritmos naturales. Formalmente, $e$ es el límite expresado como $$\lim_{n\to\infty}\left( 1 + \frac{1}{n}\right)^n$$, que es la expresión que surge al calcular el interés compuesto. Una de las propiedades más interesantes de $e$ y la que lo define es que es su propia derivada. Es decir, $$\frac{d}{dt}e^t = e^t$$ nos dice que entre más grande sea $e^t$, mayor será su tasa de crecimiento. Es ahí cuando se le llama a algo crecimiento exponencial.
• El número $i$, conocido como el número imaginario y a los números que incluyen $i$ se les conoce como números complejos.^[1] Normalmente no deberíamos ser capaces de sacar la raíz cuadrada a un número negativo. Pero los matemáticos son muy creativos y simplemente le agregaron una dimensión al plano de tal modo que ya no tenemos una línea de números, sino un plano cartesiano con arriba, abajo, izquierda y derecha. Cuando hacemos esto, ya no estamos en el plano real, sino en el plano complejo. Veremos un poco más de esto en la sección de representaciones geométricas.

De todos estos símbolos se han escrito libros enteros. No exagero.

La belleza de la ecuación anterior está en que, en el momento en el que agregamos $i$ en esta relación, estamos creando un campo vectorial que hace rotar la velocidad en 90 grados para cada posición en la que nos coloquemos en el plano.

Como vimos, $$\frac{d}{dt}e^t = e^t$$, es decir, la tasa de crecimiento de $e^t$ es la misma que su magnitud.

Entonces,

$$\frac{d}{dt}e^{it} = i\cdot e^{it}$$

Considerando que $$e^{i \cdot 0} = 1$$,

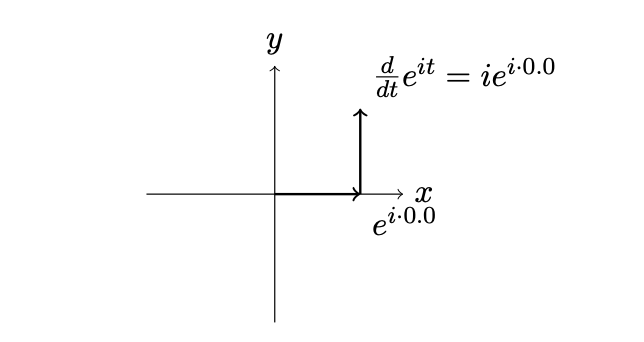
Solo hay una trayectoria comenzando en la posición (1,0) en la que la velocidad siempre coincide con el vector a una rotación de 90º: un círculo de radio 1 que va a una velocidad de una unidad por segundo. ¿Cuál es la distancia que has recorrido en el círculo después de pi segundos?

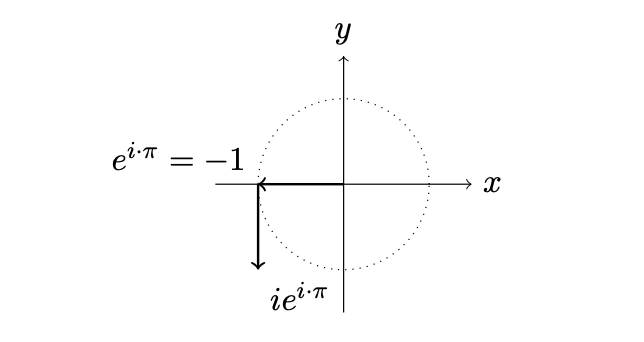
La figura anterior muestra cómo después de una rotación por la mitad del círculo, hemos recorrido pi y caemos en la posición (-1,0) de nuestro plano cartesiano. Es decir, $$e^{i\cdot \pi} = -1$$.

Pasar ese -1 del lado izquierdo de la ecuación es más un tema de estética, para asegurarnos de que los números 0 y 1 aparezcan.

Esta identidad resulta fascinante y establece el estándar de belleza para todo en las matemáticas. Y la ecuación junto con la figura harían un gran tatuaje.

1. El nombre es un poco engañoso. Ya sea que digamos que en realidad, todos los números son imaginarios o que realmente son números que sí existen y que tienen muchísimas aplicaciones en el mundo físico. ↩︎