¡Hola!
En esta entrega comenzamos con la parte técnica de nuestra serie sobre la revolución de la credibilidad.
(Lo que quiere decir: este post se ve mejor en la página porque tiene ecuaciones).
En realidad, cuando Leamer (1983) hacía una crítica a la estafa dentro de la econometría, no estaba acusando a nadie personalmente. Simplemente hacía una observación de que, si deseamos hacer que nuestros estudios sean más creíbles, necesitamos adoptar una metodología que se acerque más al método experimental.
En este post veremos:
- Un diseño clásico de un modelo de Diferecias en Diferencias de 2x2
- Notación y cómo el uso de Diferencias en Diferencias (DD) elimina el sesgo de selección.
- Y el supuesto de tendencias paralelas: la base para que el modelo DD funcione.
¿Listos?
Sigamos.
El diseño clásico de un modelo DD
Comenzaremos con un diseño clásico de 2x2:
- El tratamiento es una variable binaria. El grupo seleccionado podría haber recibido tratamiento ($D=1$) o no recibió tratamiento ($D=0$).
- El tratamiento es absorbente. Una vez que una unidad recibe el “tratamiento”, no se puede regresar a ser “no tratada”. El estado de ser tratada lo “absorbe”.
- No hay variación en el tiempo de tratamiento. Todos los grupos de tratamiento son tratados al mismo tiempo. Cuando este elemento se rompe, la complejidad del diseño aumenta muy rápido.
Ahora incluyamos un poco de notación: sea el par $(g,t)$ un grupo en un periodo particular. En el ejemplo más básico de un modelo de DD, nos interesan únicamente el grupo de control ($g_0$) y el grupo de tratamiento ($g_1$) en dos periodos ($t=1,2$). En el grupo de control, las unidades permanecen sin tratamiento durante ambos periodos, y en el grupo de tratamiento, estas pasan de no-tratadas en el periodo 1 a tratadas en el periodo 2.
Por lo tanto, tenemos 4 pares
$$ (g_1,1), (g_1,2),(g_0,1),(g_0,2) $$
Resultados Potenciales vs. Resultados Observados
Para $g\in\{g_0,g_1\}$ y $t\in\{1,2\}$, definimos $Y_{g,t}(0)$ y $Y_{g,t}(1)$ como los resultados potenciales en el grupo $g$ para el periodo $t$ con y sin tratamiento, respectivamente (cf. Plawa-Neyman, Dabrowska & Speed, 1990; Rubin, 1972). Es decir, independientemente de si es el grupo de tratamiento o control, suponemos la existencia de un contrafactual. Decimos que un resultado es contrafactual cuando el grupo al que pertenece no coincide con el resultado observado. Por ejemplo, $Y_{g_1,2}(0)$ es un contrafactual.
Si el par $(g,t)$ tiene a todas sus unidades sin tratamiento, entonces
$$ Y_{g,t} = Y_{g,t}(0) $$
Sea $D_{g,t}$ un indicador dummy que toma como valor 1 si el par $(g,t)$ recibió tratamiento, y 0 en caso contrario. Entonces podemos encontrar que
$$ Y_{g,t} = (1-D_{g,t})Y_{g,t}(0) + D_{g,t}Y_{g,t}(1) $$
Que es lo mismo que decir que $Y_{g,t} = Y_{g,t}(0)$ cuando $D_{g,t} =0$ y $Y_{g,t} = Y_{g,t}(1)$ cuando $D_{g,t} =1$.
El estimador DD y el sesgo de selección
Nos interesa estimar el efecto de tratamiento promedio en las unidades tratadas (ATT):
$$E(Y_{g_1,2}(1)-Y_{g_1,2}(0))$$
El problema es que $Y_{g_1,2}(0)$ es un contrafactual, no es el dato que realmente observamos. Podríamos intentar usar conjuntos de datos que si observamos.
- Por ejemplo, podríamos usar la diferencia entre grupos con y sin tratamiento en el segundo periodo $Y_{g_1,2}-Y_{g_0,2}$, sin embargo, el grupo de tratamiento no se determinó de manera aleatoria. Esa condición sólo se logra cuando se hace un ensayo aleatorio y se determinan los grupos aleatoriamente para evitar sesgo de selección.
- Alternativamente, podríamos usar una comparación de antes y después ($Y_{g_1,2}-Y_{g_1,1}$), pero este enfoque no nos garantiza que los cambios que observamos se hubieran dado aún sin el tratamiento.
Por lo tanto, usamos el estimador
$$ DD := Y_{g_1,2}-Y_{g_1,1}-(Y_{g_0,2},Y_{g_0,1}) $$
A este estimador se le conoce como el estimador de Diferencias en Diferencias. Su nombre lo recibe porque aplica al mismo tiempo la diferencia entre grupos y la diferencia en el tiempo. Nota que este estimador nos genera un efecto similar al de la ecuación del ATT, sin la necesidad de asignar los grupos de manera aleatoria.
Esto es lo que hace tan popular esta técnica. No es necesario hacer un ensayo aleatorio para obtener resultados similares a los de uno. Solo necesitas aplicar las diferencias entre grupos antes y después y que se cumplan algunos supuestos.
Para que DD sea un estimador confiable se requiere el supuesto de tendencias paralelas
Este es el supuesto más crítico del modelo de DD.
El supuesto de tendencias paralelas indica que, en ausencia de un tratamiento, la diferencia entre las tendencias del resultado en los grupos de tratamiento y control deberían permanecer constantes en el tiempo.
En otras palabras, si no se hubiera dado el tratamiento, el grupo $g_1$ se debería comportar igual que el grupo de control.
Visualmente se vería así:
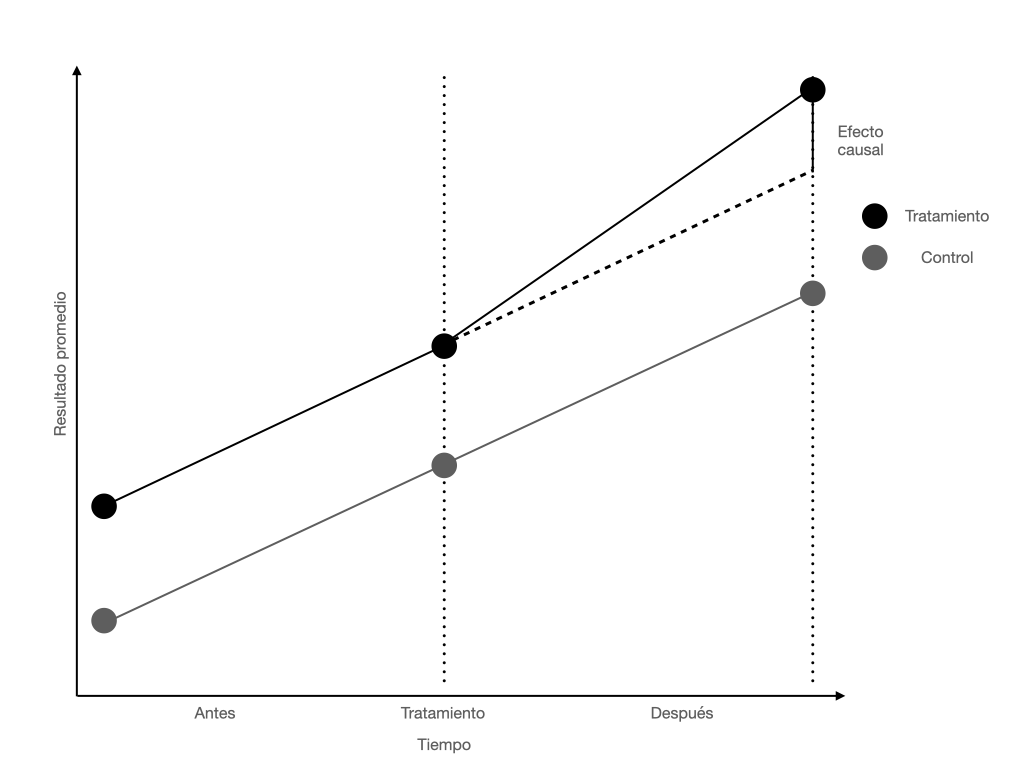
La figura nos muestra dos líneas que corren de manera paralela hasta el punto en el que se aplica el tratamiento.
La idea central del supuesto de tendencias paralelas es que, sin el tratamiento, el comportamiento de los dos grupos debería ser exactamente el mismo.
En lenguaje matemático, el supuesto de tendencias paralelas requiere que
$$ E[Y_{g_1,2}(0)-Y_{g_1,1}(0)] = E[Y_{g_0,2}(0)- Y_{g_0,1}(0)] $$
Demostración (cf. De Chaisemartin & D’Haultfœuille, 2025):
Comenzamos expresando el estimador de Diferencias en Diferencias con los resultados observados.
$$ E[DD] = E[Y_{g_1,2}-Y_{g_1,1}-(Y_{g_0,2}-Y_{g_0,1})] \\ = E[Y_{g_1,2}(1) - Y_{g_1,1}(0) - (Y_{g_0,2}(0)-Y_{g_0,1}(0))] $$
Nota que si el supuesto de tendencias paralelas aplica, podemos despejar el contrafactual $Y_{g_1,1}(0)$, y los demás términos se cancelan para dejar el mismo estimador que tendríamos en un experimento.
$$ E[DD] = E[Y_{g_1,2}(1) - Y_{g_1,2}(0)] + E[Y_{g_1,2}(0) - Y_{g_1,1}(0)] -E[Y_{g_1,2}(0) - Y_{g_1,1}(0)] \ \\ =E[Y_{g_1,2}(1) - Y_{g_1,2}(0)] $$
Referencias
De Chaisemartin, C., & D’Haultfœuille, X. (2025). Credible answers to hard questions: Differences-in-differences for natural experiments. SSRN. https://dx.doi.org/10.2139/ssrn.4487202
Leamer, E. E. (1983). Let's take the con out of econometrics. The American Economic Review, 73(1), 31–43
Rubin, D. B. (1972). Estimating causal effects of treatments in experimental and observational studies (Research Bulletin No. RB-72-39). Educational Testing Service. https://doi.org/10.1002/j.2333-8504.1972.tb00631.x
Splawa-Neyman, J., Dabrowska, D. M., & Speed, T. P. (1990). On the application of probability theory to agricultural experiments. Essay on principles. Section 9. Statistical Science, 5(4), 465–472. https://doi.org/10.1214/ss/1177012031





