Probablemente conoces modelos con datos en panel que mezclan geografía y tiempo.
Los datos en esos casos se ven algo así:
| País | Año | X | Y |
|---|---|---|---|
| México | 2021 | 1.5 | 230 |
| México | 2022 | 1.7 | 242 |
| Brasil | 2021 | 2.3 | 345 |
| Brasil | 2022 | 2.2 | 370 |
Son fáciles de identificar porque:
- Se repiten los países a través de todos los años.
- Los países y el tiempo son variables por sí mismas que agrupan características no-observables.
- El análisis involucra cómo cambia una variable en un país dado, año tras año.
Esta es una regresión en R de un modelo de panel usando efectos fijos:
library(plm)
# Datos de ejemplo
datos <- data.frame(
pais = rep(c("México", "Brasil", "Argentina"), each = 10),
año = rep(2010:2019, times = 3),
inversion_educacion = c(runif(10, 4, 6), runif(10, 5, 7), runif(10, 3, 5)),
rendimiento_escolar = c(runif(10, 450, 500), runif(10, 470, 520), runif(10, 430, 480))
)
# Convertir a panel
datos_panel <- pdata.frame(datos, index = c("pais", "año"))
# Modelo de efectos fijos
modelo_ef <- plm(rendimiento_escolar ~ inversion_educacion, data = datos_panel, model = "within")
summary(modelo_ef)
Más adelante explicamos todos los elementos. Por el momento nota que estamos usando una sintaxis muy similar a la que usaríamos en una regresión lineal con lm().
Aplicar este código es muy fácil. El único detalle que queda es entenderlo para saber cuándo y cómo usarlo.
Cuándo y cómo usar efectos fijos
No sólo hay datos en panel de países o regiones geográficas.
Los datos en panel se volvieron una forma muy popular para presentar los datos. El banco mundial te permite descargar bases de datos y acomodarlos directamente en un arreglo en panel, por ejemplo. Pero esa es una solución a un problema más viejo.
Se trata de agrupar características inobservables.
México y Perú son países diferentes [cita requerida]. A pesar de tener muchas similitudes, hay muchas características que los distinguen y que no se pueden medir tan fácilmente. Su cultura, sus leyes y su disputa por el primer lugar en quién tiene la mejor comida del planeta son sólo algunas características que los distinguen.
Son características que no siempre se pueden medir en números, pero sabemos que nos distinguen.
Lo interesante es que estas distinciones no sólo se pueden observar en países. También podríamos hacer una base de datos en panel con observaciones en el tiempo por empresa, por cliente o por individuo. Aquí estamos conjuntando todas las características que no observamos en una sola.
Por eso el estándar es llamarle individuo a cada una de estas variables características.
4 errores que cometen los econometristas novatos al usar modelos de efectos fijos
Con mucha pena te voy a contar que he cometido todos estos errores.
Y si me permites decirte, no importa que quien te lo señale sea un árbitro anónimo. Me puse rojo de vergüenza cuando me lo hicieron notar y me di cuenta.
No los vayas a cometer:
- Ignorar las variables invariantes en el tiempo. En ocasiones hay variables importantes para nuestro modelo, pero los datos disponibles no tienen mediciones en el tiempo. Si usamos un modelo de efectos fijos, todas esas variables que no varían en el tiempo se pierden cuando se hace la transformación within.
- Especificación incorrecta del modelo sin una razón teórica. Hay un modelo muy famoso para determinar si debemos usar modelo de efectos fijos o efectos aleatorios: la prueba de Hausman. Sin embargo, por si misma esta prueba no determina el tipo de modelo que se debe usar sin una justificación teórica.
- Sobreajuste con demasiados efectos fijos. Cuando te das cuenta de que incluir efectos fijos ayuda al ajuste del modelo, es fácil sentirnos tentados a incluir más, sin tener una justificación apropiada de los mismos.
- No considerar relaciones dinámicas. Hay algunas variables que por su naturaleza actúan con diferencias en el tiempo. Son los indicadores adelantados o rezagados. Aplicar efectos fijos en variables que tienen este tipo de relación dinámica en el tiempo es un error porque los efectos fijos son estáticos por naturaleza.
Guía paso a paso para usar modelos de efectos fijos
Vamos a trabajar con un conjunto de datos en panel para entender cómo aplicar un modelo de efectos fijos.
Descarga la siguiente base de datos y ejecuta el código que te daré a continuación.
Imagina que estamos interesados en analizar cómo diferentes características laborales y personales impactan los salarios de los individuos a lo largo del tiempo. En este caso, nuestro conjunto de datos incluye variables como experiencia (exp), semanas trabajadas (wks), educación (ed), y otras más. Lo interesante es que estos datos están organizados de manera que seguimos a los mismos individuos durante varios periodos, lo que nos permite controlar por características inobservables que no cambian con el tiempo.
Aquí está cómo lo hacemos:
1. Preparar los datos
Primero, es necesario cargar y preparar los datos en un formato de panel:
library(plm)
# Cargar los datos
datos <- read.csv("ruta_a_tu_archivo/panel_wage.csv")
# Convertir los datos a un formato de panel
datos_panel <- pdata.frame(datos, index = c("id", "t"))
Observa que el índice se compone de dos partes: el identificador del individuo (id) y el tiempo (t).
2. Definir el modelo de efectos fijos
El siguiente paso es definir y estimar el modelo de efectos fijos:
# Modelo de efectos fijos
modelo_ef <- plm(wage ~ exp + wks + ed + union, data = datos_panel, model = "within")
summary(modelo_ef)
Aquí estamos modelando el salario (wage) en función de la experiencia, las semanas trabajadas, la educación, y si el individuo pertenece a un sindicato. El argumento model = "within" especifica que queremos un modelo de efectos fijos, que se enfoca en la variación dentro de cada individuo a lo largo del tiempo. Esto nos permite controlar por cualquier característica inobservable que no cambie con el tiempo, como la motivación intrínseca o habilidades innatas.
3. Interpretar los resultados
Ahora que tenemos los resultados del modelo de efectos fijos, vamos a interpretarlos en detalle.
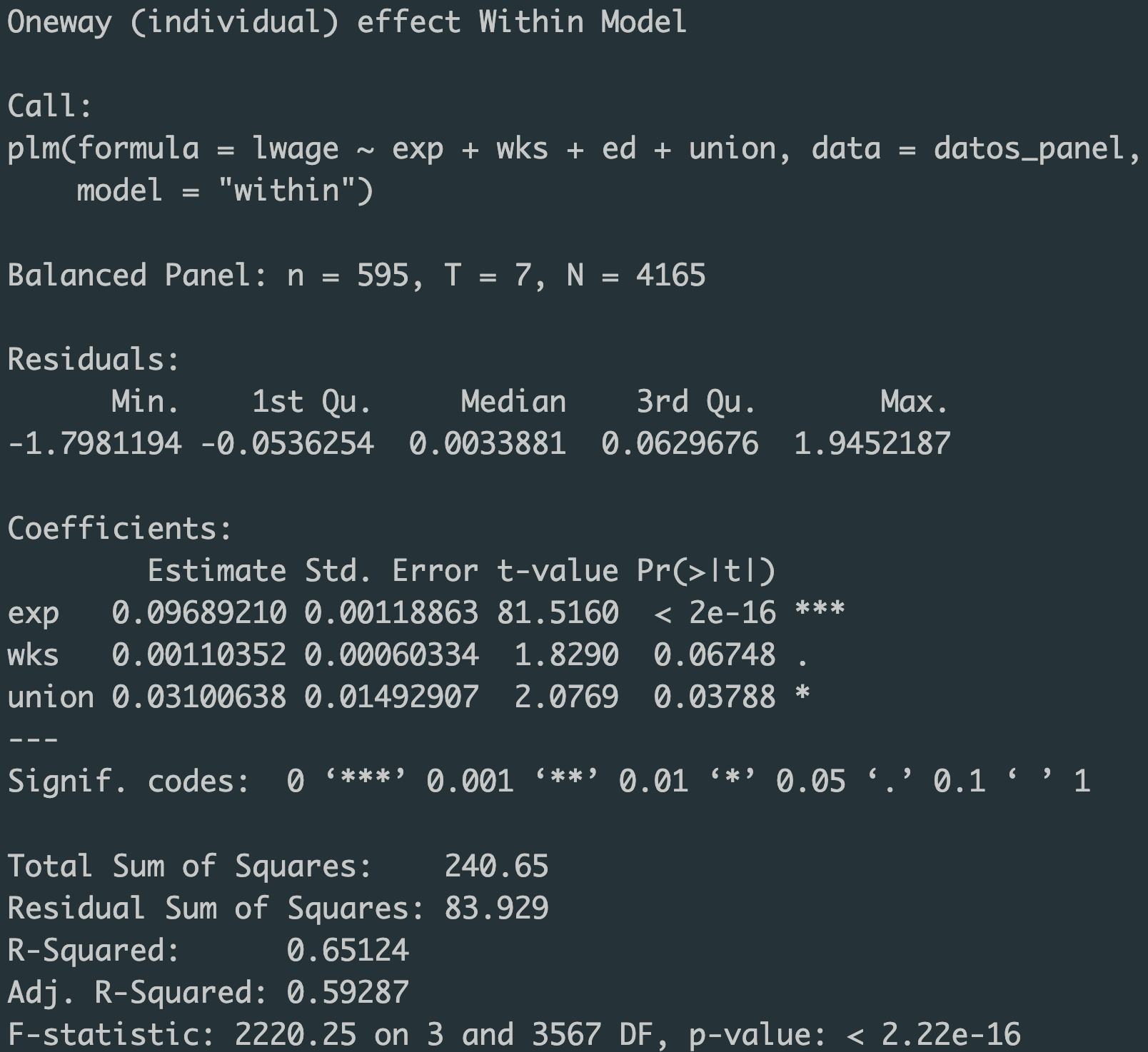
El modelo que estimamos se denomina Oneway (individual) effect Within Model, lo que significa que estamos controlando por efectos fijos a nivel individual, es decir, estamos eliminando cualquier característica invariable en el tiempo para cada individuo. El resumen del modelo nos dice que tenemos un panel balanceado con 595 individuos, observados a lo largo de 7 periodos, lo que resulta en un total de 4165 observaciones. Veamos algunos resultados clave:
- exp (experiencia): El coeficiente es 0.0969, con un valor p altamente significativo (p < 2e-16), lo que indica que un año adicional de experiencia está asociado con un aumento del 9.69% en el salario (medido en logaritmos), manteniendo constantes las demás variables.
- wks (semanas trabajadas): El coeficiente es 0.0011, con un valor p de 0.06748, lo que sugiere un efecto positivo pero marginalmente significativo de las semanas trabajadas sobre el salario.
- union (pertenencia a un sindicato): El coeficiente es 0.0310, con un valor p de 0.03788, indicando que la pertenencia a un sindicato está asociada con un aumento del 3.1% en el salario.
La R-cuadrado ajustada de 0.59287 indica que aproximadamente el 59.3% de la variación en los salarios logaritmizados se explica por las variables incluidas en el modelo, después de ajustar por efectos fijos individuales.
4. Validar el modelo
Ahora que hemos estimado nuestro modelo de efectos fijos, es crucial validar su adecuación en comparación con un modelo de efectos aleatorios.
Para hacer esto, utilizamos la prueba de Hausman, que nos ayuda a determinar si las diferencias entre los coeficientes de los dos modelos son sistemáticas.
# Estimamos el modelo de efectos aleatorios
modelo_ea <- plm(lwage ~ exp + wks + ed + union, data = datos_panel, model = "random")
# Ahora realizamos la prueba de Hausman
phtest(modelo_ef, modelo_ea)Los resultados de la prueba de Hausman para nuestro modelo son los siguientes:
- Chi-cuadrado (chisq): 8018.2
- Grados de libertad (df): 3
- Valor p: < 2.2e-16
Un valor p extremadamente bajo (menor a 2.2e-16) nos lleva a rechazar la hipótesis nula de que ambos modelos (fijos y aleatorios) son consistentes. Esto significa que el modelo de efectos aleatorios es inconsistente, y por lo tanto, el modelo de efectos fijos es el más adecuado para nuestros datos. En otras palabras, las características inobservables que son constantes en el tiempo están correlacionadas con nuestras variables explicativas, haciendo necesario el uso de efectos fijos para obtener estimaciones no sesgadas.
Con esta validación, podemos estar más seguros de que nuestro modelo de efectos fijos es el enfoque correcto para analizar los datos.
Preguntas Frecuentes
- ¿Qué pasa si mis datos no están balanceados, es decir, si algunos individuos tienen menos observaciones que otros?Esto no es un problema para el modelo de efectos fijos, ya que puede manejar paneles no balanceados. Sin embargo, debes ser consciente de que la falta de datos para ciertos individuos podría afectar la precisión de tus estimaciones.
- ¿Cómo interpreto los coeficientes si mis variables independientes también están en logaritmos?Si tanto la variable dependiente como la independiente están en logaritmos, los coeficientes se interpretan como elasticidades. Por ejemplo, un coeficiente de 0.1 implicaría que un aumento del 1% en la variable independiente está asociado con un aumento del 0.1% en la variable dependiente.
- ¿Qué hago si mi variable dependiente tiene una distribución no normal o presenta sesgo?Si la distribución de la variable dependiente no es normal, podrías considerar una transformación, como el logaritmo, para normalizarla. Si el sesgo persiste, podrías necesitar métodos más avanzados, como la regresión robusta o técnicas de mínimos cuadrados ponderados.
- ¿Puedo usar efectos fijos si tengo datos categóricos como variables independientes?Sí, puedes incluir variables categóricas como independientes. Sin embargo, ten cuidado con las variables que no varían con el tiempo dentro de cada individuo, ya que su efecto será absorbido por los efectos fijos y no podrán ser estimadas.
- ¿Cómo puedo saber si he especificado bien mi modelo?La especificación del modelo puede verificarse mediante pruebas de diagnóstico y validación, como la prueba de Hausman para decidir entre efectos fijos y aleatorios, y análisis de residuos para detectar problemas de especificación. Además, siempre es recomendable basar la especificación en una teoría sólida y en pruebas preliminares.



