¿Te imaginas tener una fórmula mágica para maximizar tus ganancias en cualquier negocio?
Pues aunque no es exactamente mágica, el método Simplex es la herramienta más cercana que tenemos para lograrlo. Este método permite encontrar el óptimo en problemas de optimización, es decir, aquellos donde queremos maximizar o minimizar algo, como ganancias o costos. La mejor parte es que, aunque la matemática detrás de él puede parecer intimidante, hoy en día una computadora puede hacer el trabajo por ti en cuestión de segundos.
Pero no se trata solo de resolver ecuaciones; se trata de entender la intuición detrás de ellas.
¿Qué es el Método Simplex y por qué deberías entenderlo?
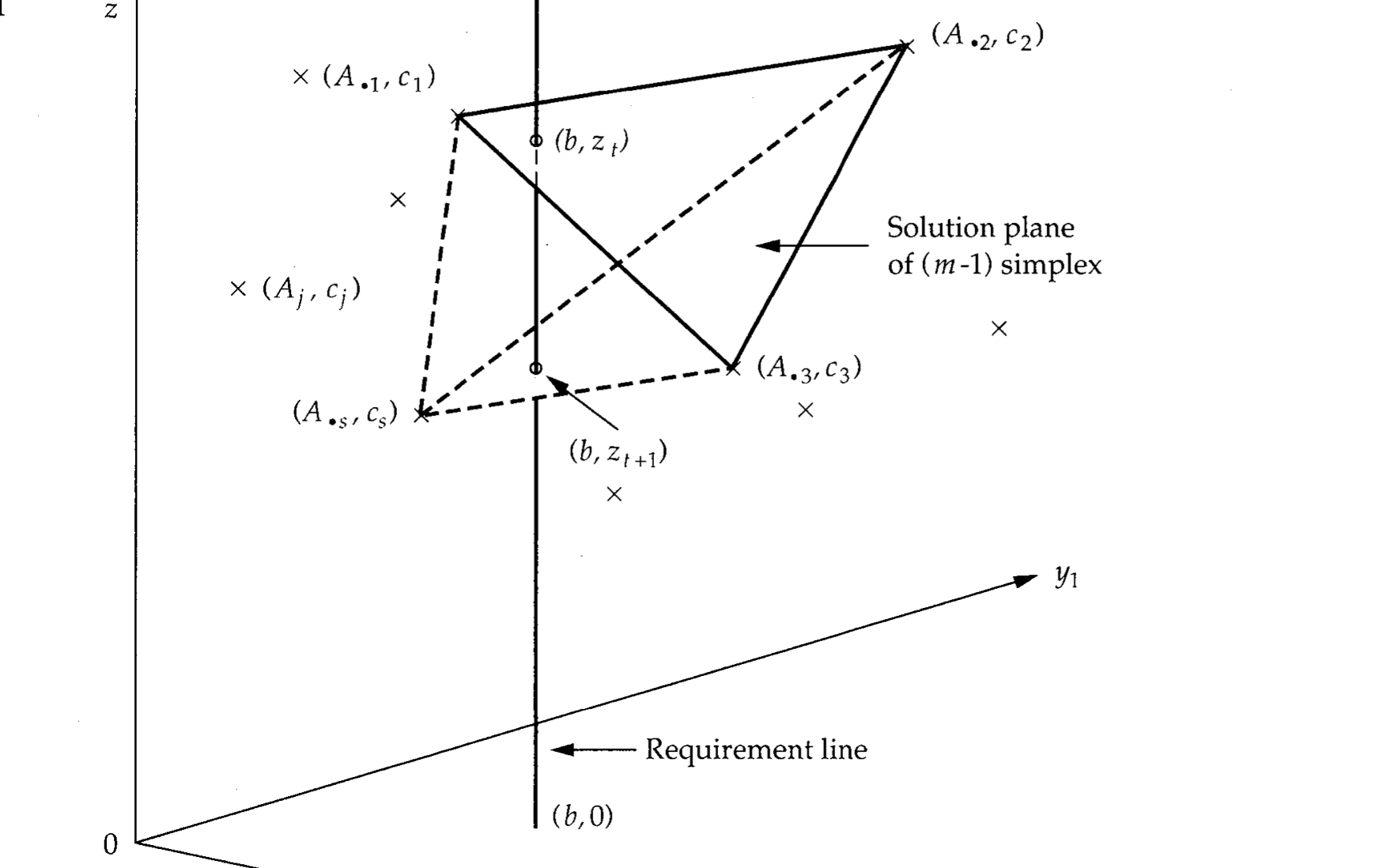
El método Simplex es una técnica matemática que resuelve problemas de optimización lineal. En términos más simples, busca la mejor solución dentro de un conjunto de soluciones posibles, moviéndose por los vértices de un espacio geométrico hasta encontrar el punto donde las ganancias sean máximas o los costos sean mínimos. Lo asombroso de este método es que, aunque el espacio de soluciones sea gigantesco, siempre se moverá por los vértices, encontrando el óptimo de manera eficiente.
¿Por qué es importante entender esto? Porque, aunque Excel puede hacer los cálculos por ti, lo que realmente te interesa es comprender por qué se llega a esa solución óptima. El método Simplex no solo es útil para problemas académicos; se aplica en la vida real, desde planear la producción en una empresa hasta optimizar la distribución de recursos en un proyecto.
La intuición detrás del Simplex
Imaginemos que tienes una pequeña granja. Tienes 3 toneladas de semillas de papa, 4 toneladas de semillas de zanahoria y 5 toneladas de fertilizante. Sabemos que cada kilo de fertilizante produce un kilo de verdura, y cada kilo de papa genera una ganancia de $1.2, mientras que cada kilo de zanahoria genera una ganancia de $1.7.
Queremos maximizar nuestras ganancias, pero estamos limitados por los recursos disponibles. Entonces, el problema se reduce a decidir cuántas papas y cuántas zanahorias sembrar para aprovechar al máximo el fertilizante y generar la mayor ganancia posible. El método Simplex nos ayudará a encontrar la combinación óptima.
El Simplex toma en cuenta las restricciones (como la cantidad limitada de fertilizante y semillas) y los coeficientes de las ganancias para determinar el mejor uso de los recursos.
Pasos para resolver el problema con Excel
Ahora que entendemos la intuición, veamos cómo resolver este problema en Excel.
- Define las variables: En este caso, las variables son las toneladas de papas (X) y las toneladas de zanahorias (Y) que vamos a sembrar.
- Especifica la función objetivo: Esta es la función que queremos maximizar, es decir, las ganancias. En este caso, sería:
$$
\text{Maximizar } Z = 1.2X + 1.7Y
$$ - Establece las restricciones: Estas son las limitaciones impuestas por los recursos disponibles. Para este problema, tenemos:
- La cantidad de fertilizante disponible: ( \(X + Y \leq 5\) )
- La cantidad de semillas de papas: ( \(X \leq 3\) )
- La cantidad de semillas de zanahorias: ( \(Y \leq 4\) )
- Introduce el problema en Excel:
- Ve a la pestaña de Datos y selecciona Solver.
- Introduce la función objetivo en una celda, utilizando las celdas para las variables X y Y.
- Define las restricciones en Solver, asegurándote de que Excel sepa que estás maximizando la función objetivo.
- Ejecuta Solver: Deja que Excel haga su magia. Después de ejecutar Solver, te mostrará la solución óptima, que será la cantidad de papas y zanahorias que debes sembrar para maximizar tus ganancias.
- Analiza los resultados: Lo más importante aquí no es solo encontrar la solución óptima, sino entender por qué esa solución es la mejor. Observa cómo el Simplex se mueve por los vértices de las restricciones hasta encontrar el punto de máxima ganancia.
La lógica del algoritmo Simplex
Ahora que sabes cómo usar el método Simplex en Excel, podrías pensar que es suficiente con dejar que la computadora haga el trabajo pesado. Pero entender el por qué detrás del algoritmo es lo que te hará destacar. El Simplex es una herramienta extremadamente poderosa, y su verdadero valor radica en que no solo te da una respuesta, sino que te muestra cómo navegar entre las diferentes opciones posibles para maximizar tus recursos.
En la vida real, este tipo de problemas se presentan constantemente. Ya sea que trabajes en una empresa que necesita optimizar su producción, o estés gestionando tus propios recursos en un proyecto, el método Simplex te ayuda a tomar decisiones informadas y estratégicas. Saber que el óptimo se encuentra en un vértice, y que el Simplex se mueve por estos puntos, te da una ventaja sobre quienes solo confían en los números sin entender lo que hay detrás de ellos.
Aplicaciones del Método Simplex en la vida real
Para que veas la utilidad del Simplex más allá de los libros de texto, aquí hay algunos ejemplos reales:
- Optimización de recursos en empresas: Imagina que una fábrica tiene recursos limitados para producir varios productos. El método Simplex les ayuda a determinar la cantidad óptima de cada producto que deben fabricar para maximizar las ganancias.
- Distribución de recursos en proyectos: Si estás gestionando un proyecto con presupuestos y plazos ajustados, el Simplex puede ayudarte a encontrar la mejor manera de distribuir los recursos para cumplir con los objetivos.
- Logística y transporte: Las empresas de logística usan el Simplex para optimizar las rutas de transporte, minimizando costos y tiempos de entrega.
¿Qué pasa cuando no entiendes el Simplex?
La mayoría de los estudiantes de economía se enfrentan a problemas como el Simplex y se sienten abrumados por los cálculos. Afortunadamente, hoy en día tenemos herramientas que nos ahorran ese trabajo, pero eso no significa que debamos ignorar la lógica detrás. Si no entiendes el método, puedes terminar confiando ciegamente en resultados que quizás no sean los mejores para tu situación específica.
Al comprender el proceso, puedes identificar cuándo un resultado no tiene sentido y ajustarlo para obtener una mejor solución.
Al final del día, se trata de entender, no solo de calcular.
Así que la próxima vez que te enfrentes a un problema de optimización, recuerda: lo más importante es entender por qué llegaste a esa solución, no solo qué solución obtuviste.






